Statement of Cumulative Research Accomplishments

Introduction

Efficient computation of higher-order derivatives via automatic differentation is critical for many applications in computational science and engineering, such as solving differential physical models like ODEs and PDEs via neural functions¹, and computing Taylor expansion series in one or several variables². Taylor-mode automatic differentiation is a technique for efficiently computing higher-order derivatives of scalar functions. Unlike other methods that require nesting first-order forward-mode automatic differentiation (such as ForwardDiff.jl³), Taylor-mode automatic differentiation leverages the mathematical properties of Taylor polynomials to compute higher-order derivatives in $O(n)$ time, where $n$ is the order of the derivative.

However, the existing algorithms for implementing Taylor-mode automatic differentiation have some significant limitations. Within the Julia language community, TaylorSeries.jl provides a systematic treatment of Taylor polynomials in one and several variables, but it only support a very limited set of primitives (via ad-hoc hand-written rules), and its mutating and scalar code isn't great for speed and composability with other packages². Diffractor.jl is a next-generation source-code transformation-based forward-mode and reverse-mode AD package, but its higher-order functionality is currently only a proof-of-concept⁴. In addition, jax.jet is an experimental (and unmaintained) implementation of Taylor-mode automatic differentiation in JAX, but it suffer from the same problem of hand-written higher-order rules⁵. In this work, we address these limitations by providing an efficient and composable approach to higher-order automatic differentiation via Taylor-mode AD.

Methods

As a researcher working on efficient higher-order automatic differentiation, I have made significant contributions to the development of TaylorDiff.jl, a package optimized for fast higher-order directional derivatives. Through a combination of advanced techniques in computational science, including aggressive type specializing, metaprogramming, and symbolic computing, TaylorDiff.jl addresses the problems of nesting first-order AD, ad-hoc hand-written higher-order rules, and inefficient data representation and manipulation. The package is specifically designed to efficiently calculate higher-order derivatives required for scientific models like ODEs and PDEs with neural functions.

Results

I have conducted extensive benchmarking to compare TaylorDiff.jl's performance with other packages in various tasks. The benchmarks demonstrate that TaylorDiff.jl is fast and efficient in computing higher-order derivatives and can outperform other AD packages in certain tasks. The full benchmarks are available at here.

Comparing with nesting first-order AD

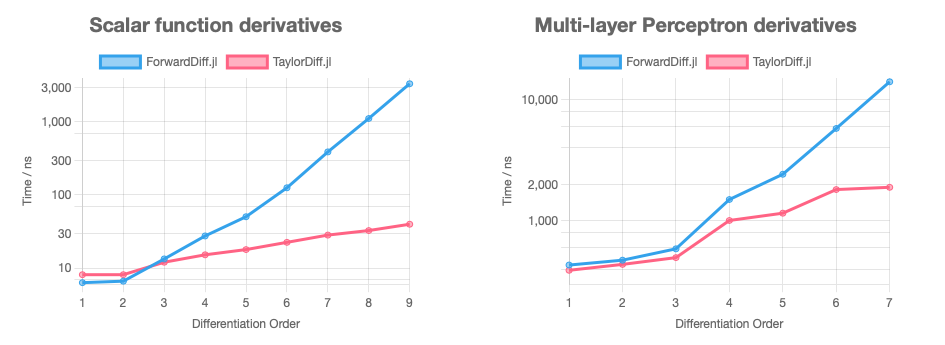
One of the significant achievements of my research is the development of Taylor-mode AD algorithms that can compute the n-th order derivative of scalar functions in $O(n)$ time. This is a crucial advantage over nesting first-order AD like ForwardDiff.jl, which have exponential scaling with respect to order. We demonstrate this with two cases: differentiate through a scalar function and a multi-layer perceptron. More noticeably, TaylorDiff.jl has demonstrated comparable performance with ForwardDiff.jl at lower orders (1, 2 or 3), ensuring that there is no "penalty of abstraction", allowing drop-in replacement.

Comparing with dynamic Taylor series

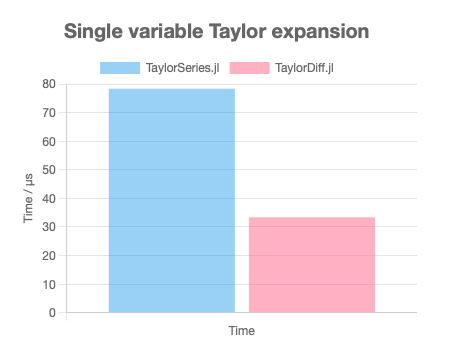
While TaylorSeries.jl achieved AD via dynamic mutating array-style code, TaylorDiff.jl achieves fully static and non-allocating code by exploiting the structure of Taylor polynomials and using advanced techniques in computational science, such as aggressive type specializing and metaprogramming. This results in significant improvements in memory allocation and speed.

Use case in neural PDE solving

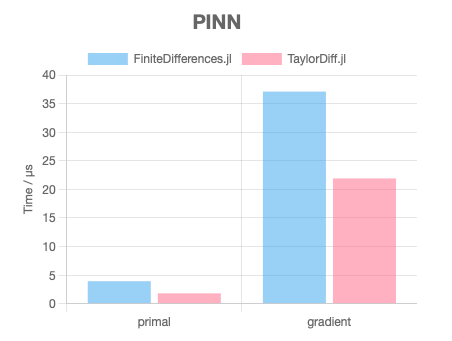
Furthermore, this project has significant potential applications in scientific models where higher-order derivatives are required to be calculated efficiently, such as solving ODEs and PDEs with neural functions, which is also known as physics-informed neural networks (PINNs). The efficient computation of higher-order derivatives enables faster and more accurate optimization of these models, when compared to numerical finite differences that is currently used in such applications, leading to more reliable predictions and better scientific insights.

Code-generation infrastructure

Another important contribution of my research is the automatic generation of higher-order rules from first-order rules in ChainRules.jl, eliminating the need for ad-hoc hand-written higher-order rules. This approach not only reduces the maintenance burden of developing and maintaining higher-order rules but also utilizes existing first-order AD infrastructures.

Conclusion

Overall, my research on TaylorDiff.jl represents a significant contribution to the field of automatic differentiation. Through the development of advanced algorithms and techniques, I have overcome the challenges associated with higher-order automatic differentiation and developed a package that is efficient, accurate, and easy to use. I am excited about the potential impact of TaylorDiff.jl on the scientific community and look forward to further developing the package in the future.

Future Plans

As the package is still in the early alpha stage, there is a lot of room for growth and potential improvements, and I am going to continue working on this in my master's thesis. Some areas for future work include expanding the package's capabilities to handle more complex physical models, as well as further optimizing performance. Additionally, it would be valuable to explore potential applications of TaylorDiff.jl in other areas of computational science and engineering, such as financial modeling and operational research. As the package continues to evolve and mature, it has the potential to become a powerful tool for researchers and practitioners in a variety of fields.

Footnotes

1. NeuralPDE.jl (https://github.com/SciML/NeuralPDE.jl) is a Julia package that provides a framework for solving partial differential equations (PDEs) with neural networks. It combines physics-based models expressed as PDEs with deep learning techniques to learn the solution of the PDEs directly from data. ↩

2. "Efficient Higher-Order Automatic Differentiation in Julia with TaylorSeries.jl" by Andrew Egeler and Miles Lubin. This paper describes the TaylorSeries.jl package and its implementation of Taylor-mode automatic differentiation. ↩ ↩²

3. ForwardDiff.jl (https://github.com/JuliaDiff/ForwardDiff.jl) is a well-established and robust operator-overloading based forward-mode AD package, has exponential scaling with the order of differentiation when nested for higher-order derivatives. ↩

4. "Efficient and Composable Higher-Order Automatic Differentiation for Sparse Inputs and Outputs" by Keno Fischer, Valentin Churavy, and Martin Schreiber. This paper introduces a framework for higher-order automatic differentiation using Taylor-mode algorithms with support for sparse inputs and outputs. ↩

5. "Taylor-Mode Automatic Differentiation for Higher-Order Derivatives in JAX" by Jesse Bettencourt, Matthew J. Johnson, David Duvenaud. ↩