跳到主要内容

薄透镜景深公式的推导

在理解景深时，可以将镜头中的镜片组简化为一片凸透镜来理解。

当相机对焦模块将镜片移动到某个位置以使物距为 uu 的物体合焦时，焦平面（物距为 uu 的所有点构成的平面）上的内容也都是合焦的。在焦平面以前或以后的一点，若在成像平面上的弥散大小小于容许弥散圆，则也可认为是合焦的。

焦距为 ff 的薄透镜的成像公式为（uu 为物距，vv 为像距）：

1u+1v=1f\frac1u+\frac1v=\frac1f

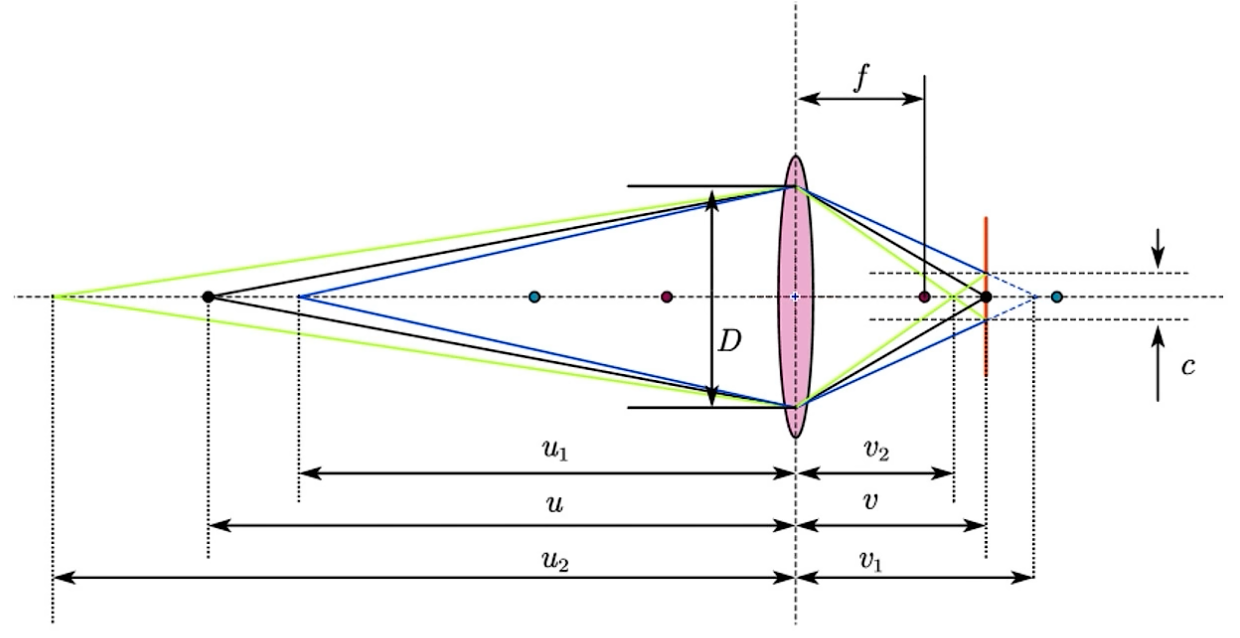
前景深和后景深的计算公式分别为

u−u1=Acu2f2+Acu,u2−u=Acu2f2−Acuu-u_1=\frac{Acu^2}{f^2+Acu},\quad u_2-u=\frac{Acu^2}{f^2-Acu}

总景深为（该公式适用条件为中等焦距、中等对焦距离，详情参考备注处的推导）

Δu=2Acf2u2f4−A2c2u2\Delta u=\frac{2Acf^2u^2}{f^4-A^2c^2u^2}

当中等焦距较远时，可以近一步简化为

Δu=2Acu2f2\Delta u=\frac{2Acu^2}{f^2}

推论：最大背景虚化​

即无穷远处点光源的成像大小，为

d=f2Aud=\frac{f^2}{Au}

而物体的放大倍率为

M=vu=fu−f≈fuM=\frac vu=\frac{f}{u-f}\approx\frac fu

若要保证物体的放大倍率基本一致，那么一个镜头的虚化能力就取决于 f/Af/A。但是在相同最大虚化的情况下：

  • 长焦：景深更深，过渡更好
  • 大光圈：景深更浅，起步快

推论：虚化和画幅的关系​

如果将拍出的照片截取中间一部分，等效于更小画幅拍出来的照片，则它最大虚化下弥散圆大小反而占整个画幅更大的比例了。但是为了获得同样的画面，在物距不变情况下实际需要更小的焦距，这个比例不仅抵消了上一个趋势，还使得实际最大虚化变小了。定量来说，影响照片回看的虚化程度是 r/Lr/L，而 r∝f2∝L2r\propto f^2\propto L^2。

推论：超焦距​

即后景深距离为无穷大，临界条件为 f2=Acuf^2=Acu 则有

u≥f2Acu\ge\frac{f^2}{Ac}

此时超焦距近限距离约为 u/2u/2。

参考文献​