广义非确定性有限自动机
阐述
形式定义
五元组 ,其中
- 是有限状态集
- 是有限字母表
- 是转换函数
- 是起始状态
- 是接受状态集
称非确定性有限自动机识别字符串 其中 是子串,如果存在 使得
阐释
GNFA 的箭头上可以写任何表达式,每次读取一段输入而非一个字符,方便起见规定
- 开始状态 有去向任何其他状态的箭头,但没有入箭头
- 结束状态 (单个)有所有其他状态的入箭头,但没有出箭头
- 除了这两个状态,其他任何状态和任何状态之间都有箭头,包括自身
实例
性质
相关内容
有限自动机转换为 GNFA
- 添加一个新的起始状态,用 指向起始状态
- 添加一个新的接受状态,旧的接受状态以 指向
- 把箭头上的多个符号变成一个集合
- 将没有相连的状态上加入
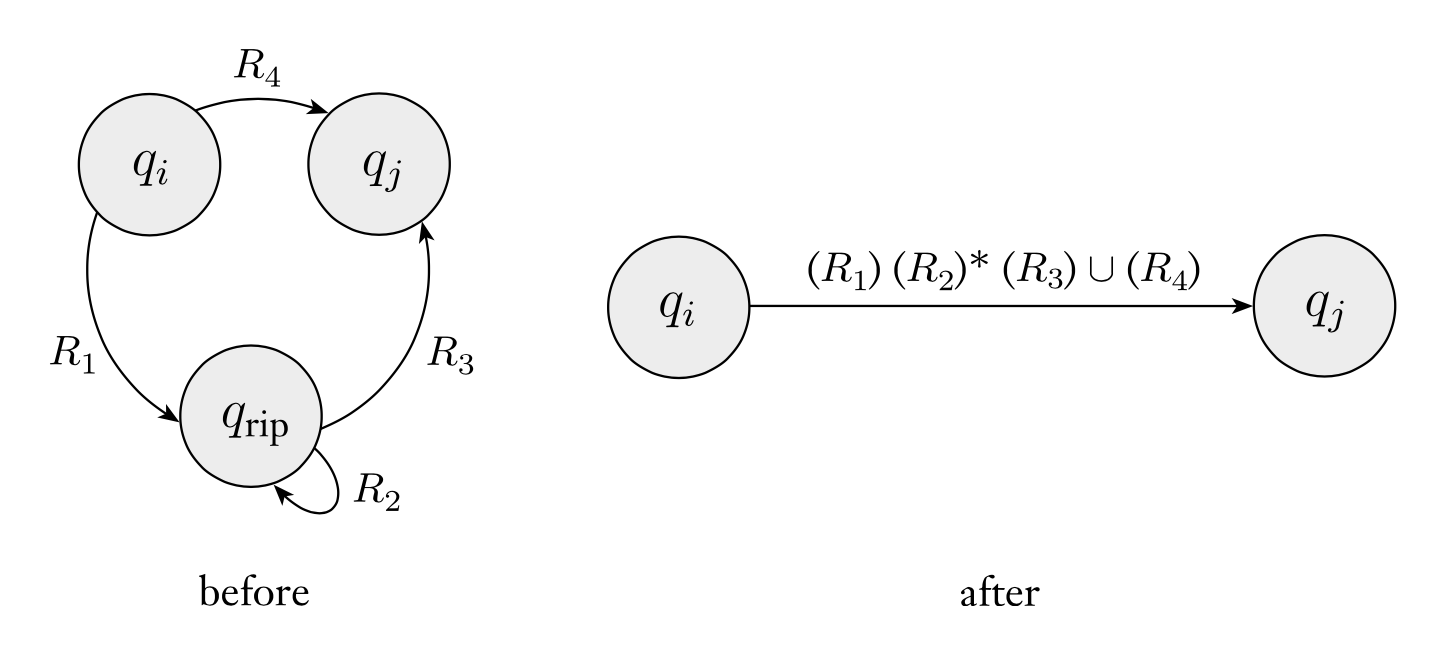
GNFA 转换为正则表达式
- ,直接读取箭头上的正则表达式
- ,选择一个状态去除掉,然后在其他的通过这个状态的两个状态之间改变正则表达式