有限自动机
阐述
形式定义
五元组 ,其中
- 是有限状态集
- 是有限字母表
- 是转换函数
- 是起始状态
- 是接受状态集
称有限自动机识别字符串 ,如果存在 使得
阐释
本质是对于内存非常有限的计算机的模型,其内存完全来自于系统处于哪一个状态。
如何设计有限自动机
将自己放在机器的位置,思考自己如何用一种机械化的方式完成机器的任务。对于任何一个字符串,我们必须一个接一个地接收其中的字符,并在每个字符之后都马上给出该部分字符串是否符合的答案。
- 思考如何记住目前已看到字符串中的关键信息
- 将关键信息表示为几种可能性,为每个可能性关联一个状态
- 补充每读取一个字符将如何在这些状态中转换
- 标记初始状态和接受状态
实例
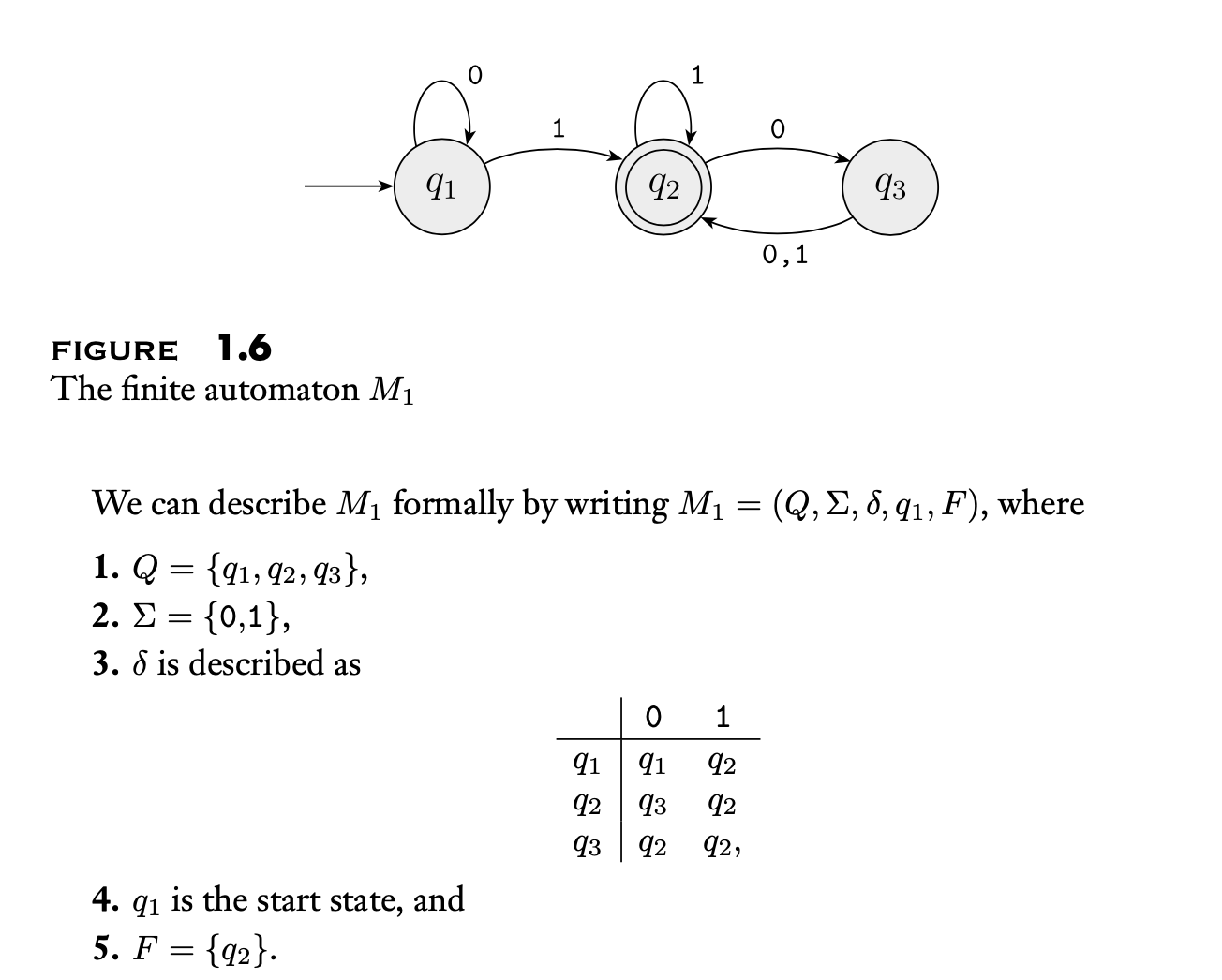
性质
相关内容
有限自动机可以扩展为非确定性有限自动机,但它们的计算能力是等价的。