浮点数

阐述

浮点数是指在计算机中用一个小数部分和可变的整数部分来近似表示实数的办法。

浮点数的通式是：

$$\pm (d_0+d_1\beta^{-1}+\cdots+d_{p-1}\beta^{-(p-1)})\beta^e,\quad 0\le d_i<\beta$$

• 基数 $\beta$
• 精度 $p$
• 指数范围 $[e_{\min},e_{\max}]$
• 如果 $d_0\ne 0$，则这个数是正常的

两个浮点数之间的间隔与数字的大小有关，并且据此定义了机器精度。

特殊数值

特殊数值包括 $\pm\infty,\mathrm{NaN}$。他们满足：

• 溢出操作返回 $\pm\infty$
• $x/\pm\infty=0$，并且 $x/0=\pm\infty$
• 涉及到无穷大的运算看作是极限
• 如果极限不存在，返回 NaN

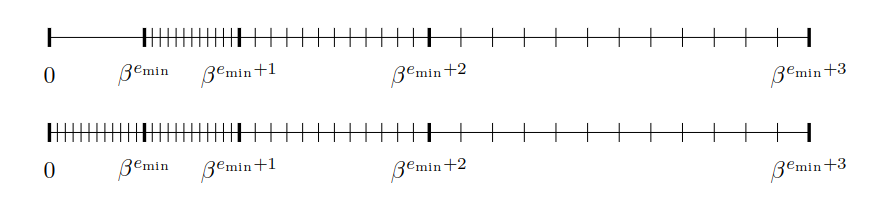
非正常数

正常数的问题在于，在 0 和 \beta^{e_\min} 之间有个空隙，这会导致 $x-y=0$ 即使 $x\ne y$。为了解决这个问题，我们让 e_\min 指数下浮点数的表示可以有 $d_0=0$，这样在对数意义上下溢出是平滑的。

实例

IEEE 单精度浮点数

32 位包括 1 符号，8 指数和 23 小数，表达的正常数（$0<E<255$）为

$$(-1)^S\times 1.M\times 2^{E-127}$$

其余情况为

• $E=0,M=0$: 表示 $\pm0$
• $E=0,M\ne 0$: 表示非正常数，此时指数视为 $2^{-126}$
• $E=255,M=0$: 表示 $\pm\infty$
• $E=255,M\ne0$: 表示 NaN

IEEE 双精度浮点数

64 位包括 1 符号，11 指数和 52 小数，指数偏移量为 $-1023$.

性质

浮点数运算

对任何实数 $x$，最接近的浮点数表示满足 $\operatorname{fl}(x)=x(1+\varepsilon)$，其中 $|\varepsilon|<\varepsilon_{\rm machine}$。

设 $+,-,\times,\div$ 分别用 $\odot$ 来表示对应的浮点数运算，那么满足

2. $x\odot y=(x\cdot y)(1+\varepsilon)$，其中 $|\varepsilon|<\varepsilon_{\rm machine}$
3. 不仅如此，而且满足 $x\odot y=\operatorname{fl}(x\cdot y)$；后者被称为正确的舍入或者精确的舍入。这意味着浮点运算总是等价于先进行精确的运算然后舍入到最近的浮点数值。也就是说，

1.0 + 1.0 == 2.0

这样的代码总是正确的，不会有某些随机的误差。

无结合性

浮点数运算不具有结合性，也就是 $(x\odot y)\odot z\ne x\odot(y\odot z)$，其中 $\cdot=+,\times$。例如

1.0 + (-1.0 + 1e-100) # 0.0

在某些情况下，这需要我们认真考虑到底应该如何安排计算顺序。例如

• $e^x-1$ 与 expm1 函数
• 二次方程求根公式
• 大数组求和

相关内容

参考文献