Turing 机

阐述

在实际使用中，我们几乎从来不给出 Turing 机的形式定义。

形式定义

七元组 $(Q,\Sigma,\Gamma,\delta,q_0,q_{\rm accept},q_{\rm reject})$，其中

• $Q$ 是有限状态集合，$q_0,q_{\rm accept}\ne q_{\rm reject}$ 在其中
• $\Sigma$ 是有限输入字母表，不含有空格
• $\Gamma$ 是有限条带字母表，且 $s\in\Gamma$，$\Sigma\subseteq\Gamma$
• $\delta:Q\times\Gamma\to Q\times\Gamma\times\{L,R\}$ 是转换函数

组态

称当前的状态、条带内容和指针位置为一个组态。组态的记法是 $uqv$，其中 $uv$ 是条带的内容，而指针处于 $v$ 的第一个字符上。

• 起始组态是 $q_ow$
• 接受组态是包含 $q_{\rm accept}$ 的组态
• 拒绝组态是包含 $q_{\rm reject}$ 的组态
• 接受组态和拒绝组态都会使 Turing 机停机，不会继续演化

计算过程

称 $M$ 接受 $w$ 如果存在一个组态序列 $C_1,\cdots,C_k$，

• $C_1$ 是 $q_0w$
• $C_i$ 生成 $C_{i+1}$
• $C_k$ 是接受组态

阐释

一开始，输入 $w=w_1\cdots w_n\in\Sigma^*$ 在最左边的 $n$ 个方块上，其余位置都是空格，指针也在最左边，然后根据 $\delta$ 的运算规则移动，直到进入接受、拒绝态。

与有限状态自动机的区别：

1. Turing 机可以读写纸带
2. 读写头可以向左或向右移动
3. 纸带在一端是无穷长的
4. 接受和拒绝状态可以随时进入

性质

• 如果存在一个 Turing 机识别一个语言，则称它是 Turing 可识别语言
• 对所有输入都会停机的 Turing 机称为判定者
• 如果存在一个判定者识别一个语言，则称它判定一个语言，语言是 Turing 可判定的，或可判定语言

实例

以下 Turing 机 $M$ 可以判定 $B=\{w\verb|#|w\mid w\in\{0,1\}^*\}$:

性质

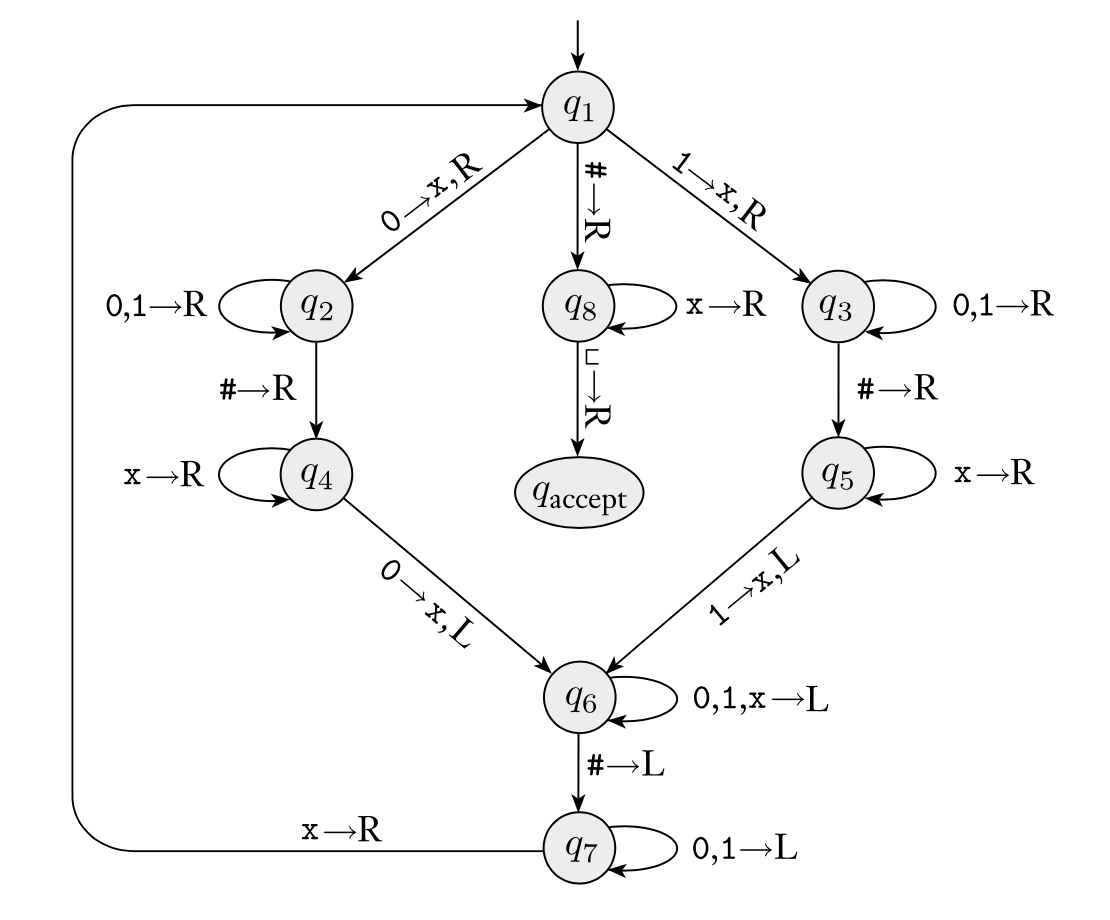
相关内容

Turing 机的几种等价变体：

1. 多个纸带：$\delta: Q \times \Gamma^{k} \longrightarrow Q \times \Gamma^{k} \times\{\mathrm{L}, \mathrm{R}, \mathrm{S}\}^{k}$
2. 非确定性：$\delta: Q \times \Gamma \longrightarrow \mathcal{P}(Q \times \Gamma \times\{\mathrm{L}, \mathrm{R}\})$
   1. 只要任一个分支接受了一个输入，就称这个 NTM 接受了输入
   2. T-可识别与 NT-可识别等价，T-可判别与 NT-可判别等价
3. 枚举器：一个具有无限长的工作纸带并能将字符串输出的机器
   1. 一个语言是 T-可识别的当且仅当它可以被一个枚举器枚举出来

参考文献