上下文无关文法

阐述

形式定义

四元组 $G=(V,\Sigma,R,S)$，其中

• $V$ 是变量的有限集

• $\Sigma$ 是终结符的有限集

• $R$ 是规则的有限集，每条规则将一个变量替换为一个由变量和终结符构成的字符串或 $\varepsilon$

• $S\in V$ 是起始变量

• $u$ 生成 $v$（$u\Rightarrow v$）：通过单步替换可以得到

• $u$ 推出 $v$（$u\Rightarrow^*v$）：通过多步替换可以得到

性质

由它生成的语言 $L(G)=\{w\in\Sigma^*|S\Rightarrow^*w\}$ 称为上下文无关语言。

上下文无关文法可以用 Chomsky 范式 表达。

上下文无关文法与非确定性的下推自动机等价。

设计

1. 将给定的语言分解为几个语言的并集，然后添加新的起始变量
2. 如果是正则语言，可以用 DFA 转化而来（见下）
3. 使用类似于 $R\to uRv$ 的语法来让字符串的不同部分保持关联

模糊性

最左推导：推出 $w$ 的过程中每次都是替换最左端的变量

• 如果 $w$ 有两个或更多的最左推导，则它是模糊的
• 如果存在一个 $w$ 是模糊的，则 $G$ 是模糊的
• 有些 CFL 只能用模糊语法生成，称它是内在模糊的

实例

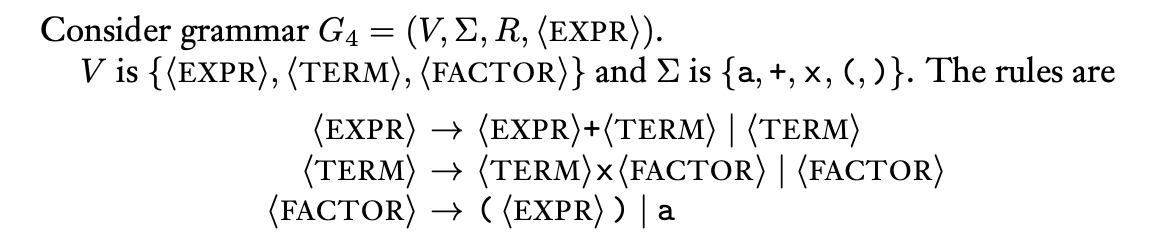
性质

相关内容

正规语言的上下文无关文法

先构建出正规语言的有限状态自动机，然后

• 对每个状态 $q_i$ 定义一个变量 $R_i$，特别地定义 $R_0$ 对应于起始状态 $q_0$
• 如果 $\delta(q_i,a)=q_j$，添加规则 $R_i\to aR_j$
• 如果 $q_i$ 是接受状态，添加规则 $R_i\to\varepsilon$

参考文献