形式定义
六元组 M=(Q,Σ,Γ,δ,q0,F),其中
- Q 是状态的有限集
- Σ 是输入的字母表
- Γ 是栈的字母表
- δ:Q×Σε×Γε→P(Q×Γε) 是转换函数
- q0∈Q 是起始状态
- F⊆Q 是接受状态
运算过程:接受 w,如果 w=w1w2⋯wm,其中 wi∈Σε,状态 r1,⋯,rm∈Q,字符串 s0,⋯,sm∈Γ∗ 满足
- r0=q0,s0=ε
- (ri+1,b)∈δ(ri,wi+1,a),其中 si=at,si+1=bt 对于某些 a,b∈Γε
- rm∈F
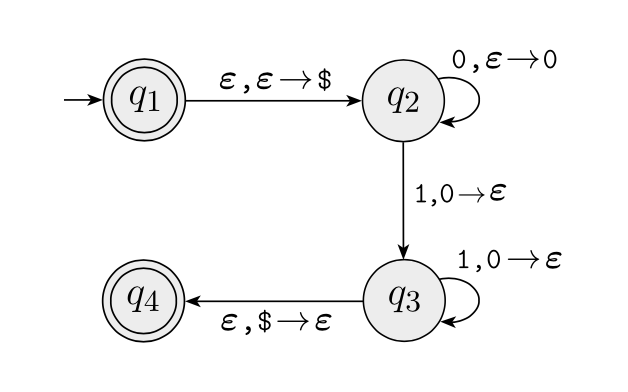
在图上,a,b→c 意味着读取 a,并且将栈顶的 b 替换为 c。它们都可以是 ε:
- a=ε 意味着不需要读取即可行动
- b=ε 意味着不需要从栈顶弹出
- c=ε 意味着不需要向栈顶压入
下推自动机具有无限的内存,但是只能对栈的顶端进行弹出和压入操作。
下推自动机与上下文无关文法等价。
这个 PDA 可以识别语言 {0n1n∣n≥0}:
相关内容
参考文献