跳到主要内容

非确定性有限自动机

阐述​

形式定义​

五元组 (Q,Σ,δ,q0,F)(Q,\Sigma,\delta,q_0,F)，其中

  • QQ 是有限状态集
  • Σ\Sigma 是有限字母表
  • δ:Q×Σε→P(Q)\delta:Q\times\Sigma_\varepsilon\to P(Q) 是转换函数
  • q0∈Qq_0\in Q 是起始状态
  • F⊆QF\subseteq Q 是接受状态集

称非确定性有限自动机识别字符串 w=y1⋯ymw=y_1\cdots y_m，如果存在 r0,⋯ ,rm∈Qr_0,\cdots,r_m\in Q 使得

  1. r0=q0r_0=q_0
  2. ri+1∈δ(ri,yi+1)r_{i+1}\in\delta(r_i,y_{i+1})
  3. rm∈Fr_m\in F

阐释​

与有限自动机的两个核心区别：

  • 一个状态对于一个字符可以有零、一或多个出箭头
  • 一个状态可以有零、一或多个出箭头上写着 ε\varepsilon

它运转的逻辑：

  • 每次遇到多种选择，它分叉为多个自己的拷贝并且并行完成剩余的计算
  • 每次遇到一个带有出箭头 ε\varepsilon 的状态，它分叉为多个自己的拷贝，其中一个停在原地，其余跟随出箭头到达下一个状态
  • 如果对当前字符没有任何出箭头，则认为该分支终止
  • 如果有任何分支接受了字符串，则认为机器接受了字符串

实例​

性质​

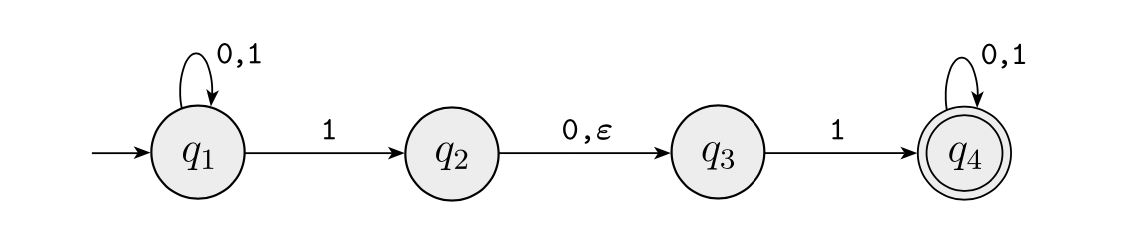
相关内容​

DFA 和 NFA 的等价性​

对于 NFA N=(Q,Σ,δ,q0,F)N=(Q,\Sigma,\delta,q_0,F)，构造 M=(Q′,Σ,δ,q0′,F′)M=(Q',\Sigma,\delta,q_0',F')：

  • Q′=P(Q)Q'=P(Q)
  • δ′(R,a)=∪r∈RE(δ(r,a))\delta'(R,a)=\cup_{r\in R}E(\delta(r,a))
  • q0′=E({q0})q_0'=E(\{q_0\})
  • F′={R∈Q′∣R∩F≠∅}F'=\{R\in Q'|R\cap F\ne\emptyset\}

其中 E(R)E(R) 是从 RR 出发仅经过 ε\varepsilon 就可以达到的状态。

参考文献​