约束规划

阐述

约束规划是指使用约束来限制决策变量可以取的值。这种方法可以精细地刻画问题的子结构，并且把尽可能多的关于问题的结构告诉求解器，从而求解器可以自动探索问题。

可满足性问题

一般来说，约束规划把需要做出的决策排成一个顺序，然后

• 在剩余的决策空间中作出决策
• 将新的决策进行约束传播，直至不动点
  • 检查约束是否都能被满足
  • 利用已知的信息来减少下一个决策的空间
  • 在一个约束编程的系统中，每一种约束都有一个专门的算法来做这两件事情
• 决策可能是错误的，如果无法满足约束，就回溯到上一个决策

优化问题和可满足性问题的关系

约束规划主要着眼于约束。

首先通过求解一系列可满足性问题来取得一个解，然后增加一个「需要比当前的解更好」的条件，继续搜索。

理论上它可以找到最优方案，但只有在新约束可以很好地减小搜索空间的时候好用

约束传播

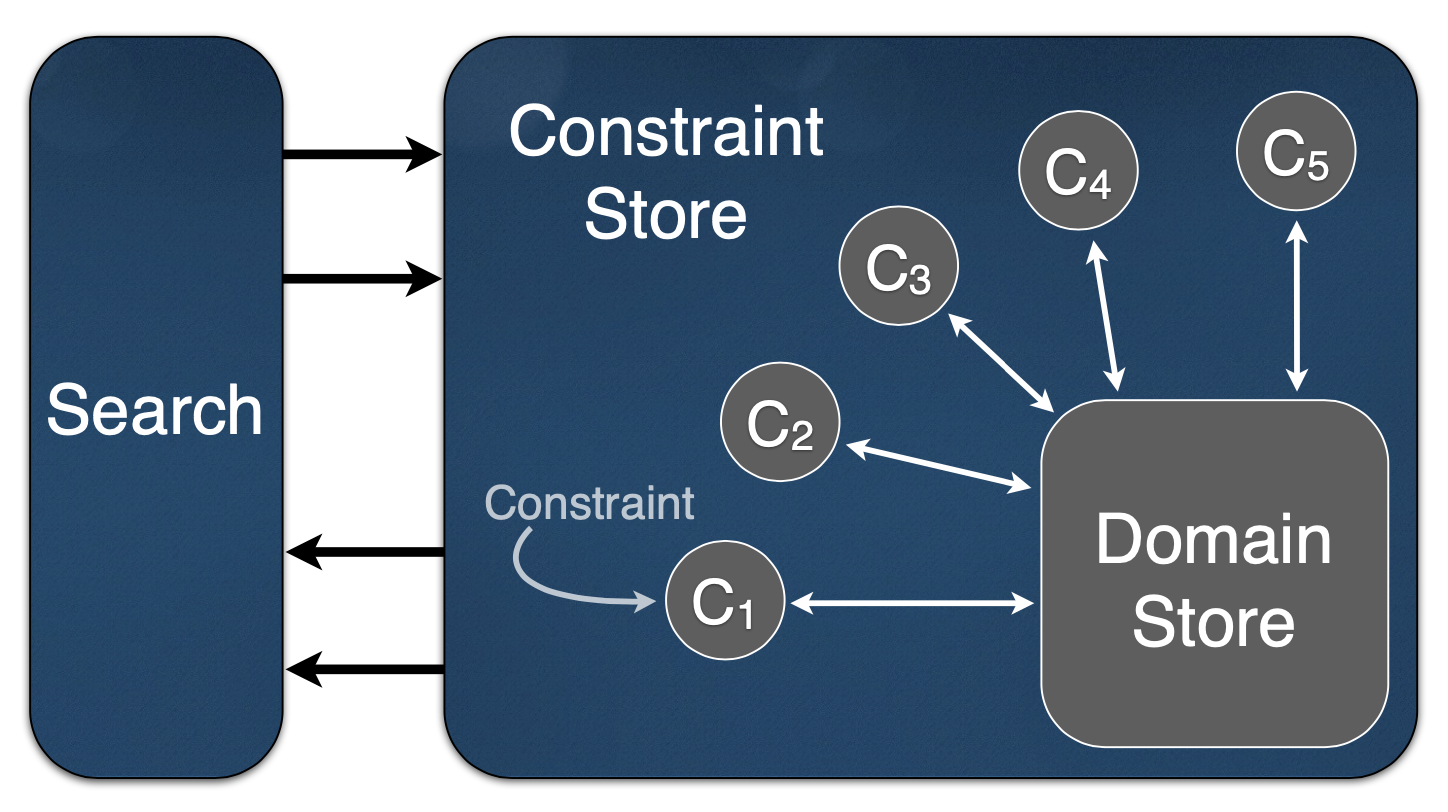
约束传播本质上类似于一个不动点算法：

• 每次选一个约束 $c$
• 如果 $c$ 在当前的域下不可行，返回失败
• 运行 $c$ 的剪枝来更新可行域
• 直到没有任何新的约束可以用来剪枝，返回成功

实例

线性约束

对于如下的线性约束：

$$a_1x_1+\cdots+a_nx_n\ge b_1y_1+\cdots+b_my_m$$

其中 $a_i,b_j>0$，则

• 可行性测试：$\sum_ia_iD^+(x_i)\ge\sum_ib_iD^-(x_i)$，并且我们把这两边分别记为 $l,r$
• 剪枝：
  • $x_i\ge\lceil (r-(l-a_iD^+(x_i)))/a_i\rceil$
  • $y_j\le\lfloor(l-(r-b_jD^-(y_j)))/b_j\rfloor$

重化

重化是指将一个约束变换为一个二值的变量，如果结束为真则值为 1，否则为 0。

这等价于引入一个新的变量 $b$，并且加以约束：

$$\operatorname{booleq}(b,x,v)\Leftrightarrow(b=1\wedge x=v)\vee(b=0\wedge x\ne v)$$

元素约束

可以用变量或者变量的表达式来索引一个数组，例如 $x=c[y]$

约束的逻辑结合

可以用 $\Rightarrow$ 来连接两个约束

全局约束

全局约束是指能揭示问题的某种全局结构的约束，它可以把问题结构更清晰地告诉求解器，这样就不用再次发现这些结构。全局约束在一定程度上解决了约束之间独立检验、不能相互交流的问题，可以更好地检验可行性或者剪枝。

• alldifferent：多个变量各不相同
• 表格约束：多个变量组合起来只能取特定的组合值，不是独立的

冗余约束

冗余约束是在语义上冗余（不排除任何解）但是计算上有价值的约束

1. 表达解的某种性质，从而更好地传播约束
2. 提供一个更高的视角，结合现有的约束，从而提高沟通

性质

对称性破缺

有时候问题中存在对称性，如果不加以注意，有可能会出现重复搜索的情况。通常的解决办法是增加一些额外的约束，以使得不重复进行这些约束，这被称为对称性破缺。

相关内容

• 八皇后问题

参考文献