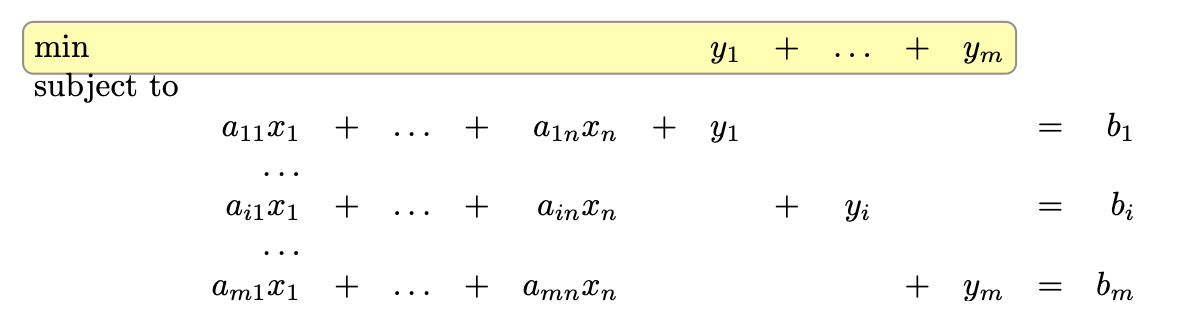单纯形法

阐述

单纯形法是求解线性规划的一种方法。它要求问题输入为标准形式：

$$\min c^Tx;~\mathrm{s.t.}~Ax=b;x\ge0$$

它可能的输入有三种：

• 不可行
• 无界
• 一个最优的基本可行解

基本思路

1. 最优解一定是在顶点上；
2. 顶点是一个基本可行解；
3. 有办法从一个基本可行解移动到另一个基本可行解；
4. 可以检验当前的基本可行解是不是最优的。

单纯形法实际上是一种局部搜索，从一个基本可行解移动到另一个基本可行解，但是可以保证一定会收敛到最优解。

移动

我们想找到一个非基本变量 $x_j$，然后令 $d_j=1,d_{N\ne j}=0$，移动 $x\to x+\theta d$。此时，约束给出 $d_B=-B^{-1}A_j$。若定义约化 $\bar c=c-c_B^TB^{-1}A$，则相应的系数就是移动单位长度获得的收益。因此，如果 $\bar c\ge0$，则证明已经达到了最优解。

下面我们考虑应该取多少步长。如果 $d\ge 0$，则无论怎么移动都合法，问题是无界的；如果不是这样的话，计算

$$\theta^*=\min_{i:d_{B(i)}<0}\frac{x_{B(i)}}{-d_{B(i)}}$$

收敛

1. 如果所有 BFS 都不简并，则一定能在有限步内收敛到最优解
2. 如果存在简并，则可能导致循环，此时需要仔细选择哪些变量进入或者离开了基本变量
   1. 例如，选择最小的 $\bar c_j<0$；在可以离开的变量中选择下标最小的。

寻找第一个基本可行解

先求解这个问题

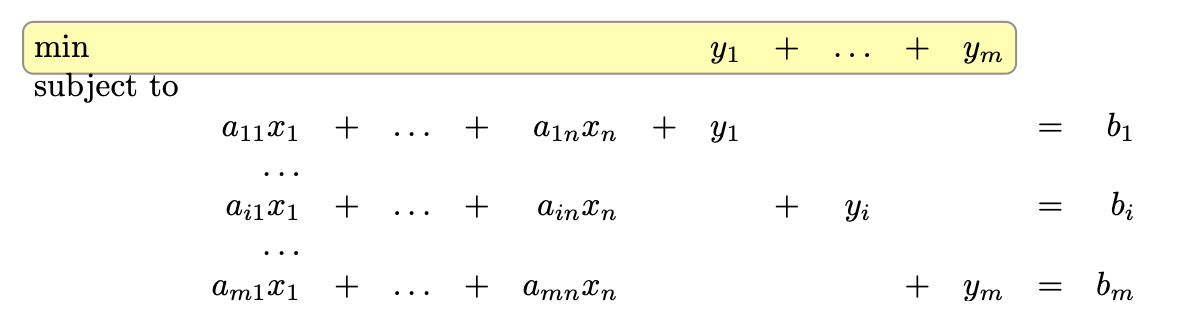
如果最优目标函数值能达到 0，则有基本可行解；否则原问题不可行。

表格形式

$$\begin{pmatrix} -c_B^TB^{-1}b&c-c_B^TB^{-1}A\\ B^{-1}b&B^{-1}A \end{pmatrix}$$

实例

性质

相关内容

参考文献