一个 n 维的微分流行是一个集合 M 以及一组单射 xα:Uα⊂Rn→M,使得
- ⋃αxα(Uα)=M
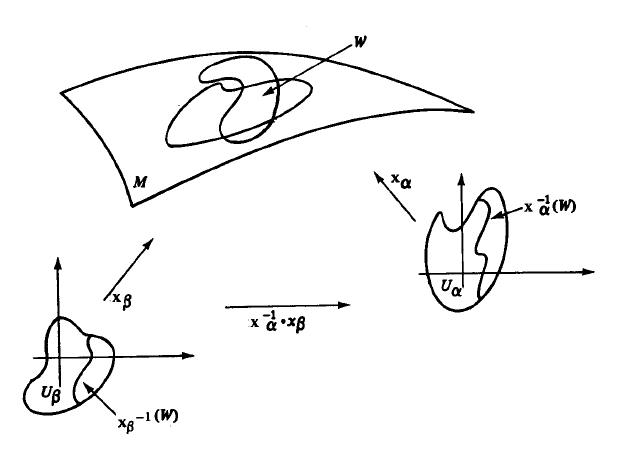
- 对于两个映射的值域交集 xα(Uα)∩xβ(Uβ)=W=ϕ,它们对应的原像 xα−1(W) 和 xβ−1(W) 仍然是开集,而且 xβ−1∘xα 是可微的
- {(Uα,xα)} 是最大的
其中每一个对 (Uα,xα) 称为一个集合 M 中点 p 的参数化,它的值域称为坐标邻域。所有的对合起来称为一个微分结构。
微分结构导致了一个自然的 M 的拓扑:A⊂M 是开的当且仅当 xα−1(A∩xα(Uα)) 是开的。
微分流形的映射
称 φ:M1→M2 在 p 点是可微的,如果存在一个参数化 y:V⊂Rm→M2 和一个参数化 x:U⊂Rn→M1 使得
y−1∘φ∘x:U⊂Rn→Rm
在 x−1(p) 是可微的。这个条件并不依赖于参数化的具体形式。称这个实数空间的映射是一个表达。
Euclidean 空间和恒等映射是一个微分流形的平凡例子。
实投影空间
Rn+1 中所有方向构成的集合是一个 n 维微分流形。
相关内容
参考文献
