稀疏直接解法

阐述

对线性方程 $Ax=b$ 当 $A$ 是稀疏数组时直接求解。本质上类似于 LU 分解或者 Cholesky 分解，但是保留了矩阵的稀疏性。这通常需要通过对变量重新排序来实现。

稀疏矩阵一般只存储非零元，存储 $\Theta(k)$，计算矩阵向量乘法也只需要 $\Theta(k)$。

图表示

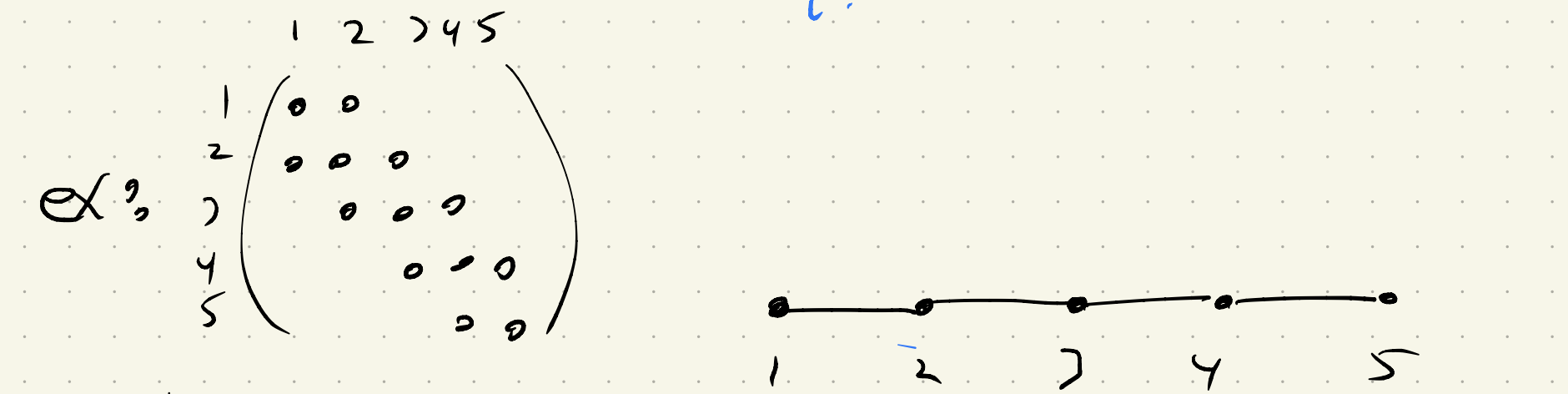
对称矩阵可以用无向图表示，而非对称矩阵可以用有向图表示。本质上说，重新排序就是将这个图切分成几片，它们之间通过比较少的边相连。

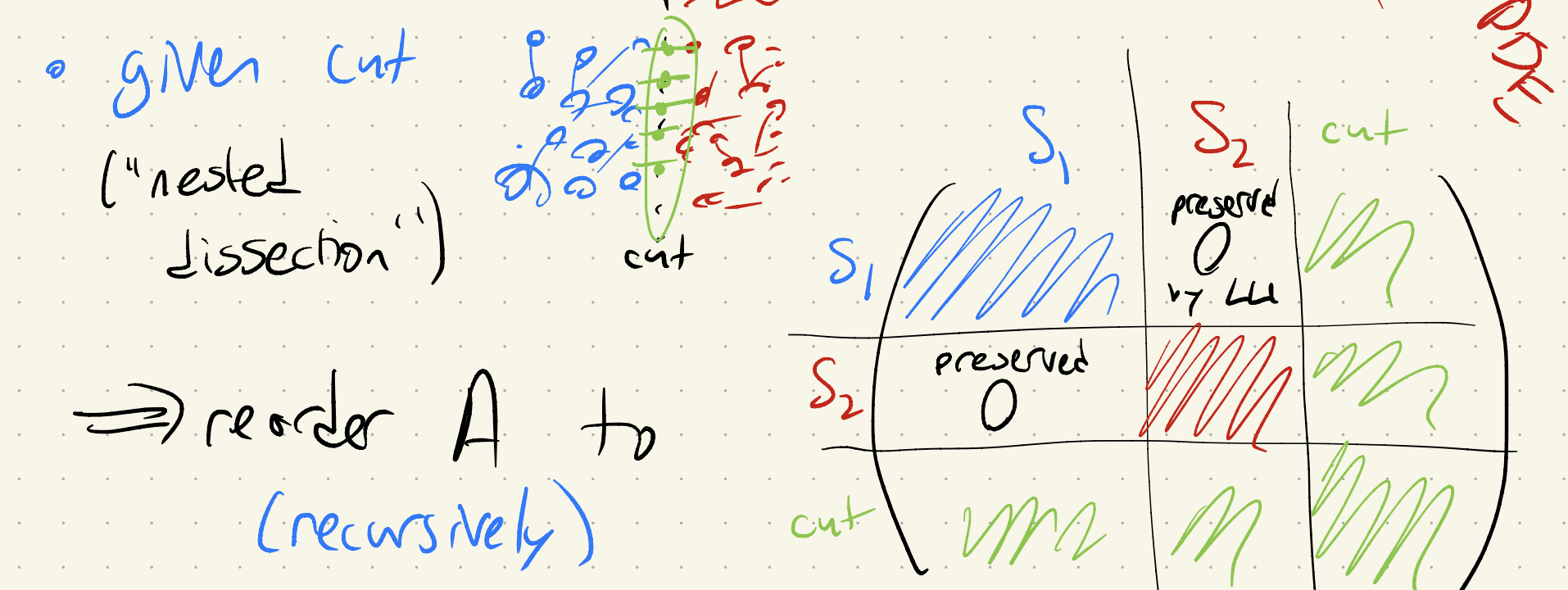
图的结构通常和矩阵的来源有关，例如一维、二维和三维的 PDE 离散化之后通常会得到具有一维、二维和三维的图。

维数	空间	时间
1	$O(N)$	$O(N)$
2	$O(N\log N)$	$O(N^{3/2})$
3	$O(N^{4/3})$	$O(N^2)$

实例

性质

相关内容

参考文献