缓存优化
对于很多算法来说,只分析浮点计算次数(flops)不足以解释性能的差异。
阐述
建立如下的理想缓存模型:
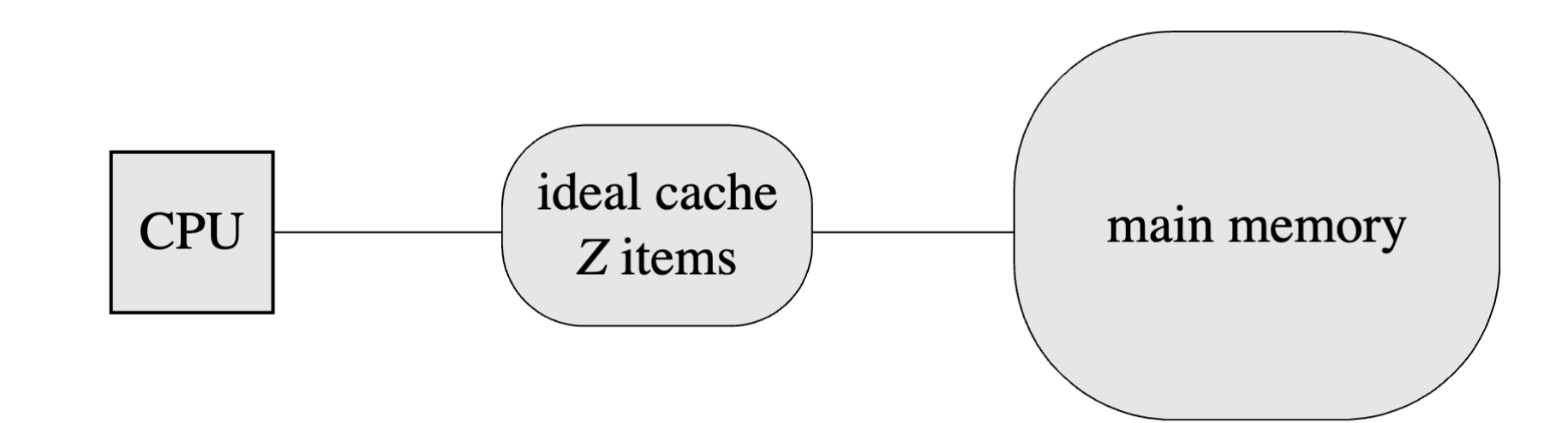
如果 CPU 需要的数据在缓存中,则称为缓存命中,速度很快;否则,从内存中拿取该数据,并替换掉缓存中原来的某个数据。
- 理想替换:替换掉未来不再被使用的时间最长的数据
- LRU 替换:替换掉过去没有被使用的时间最长的数据
- 时间局部性:同一个数据在一段时间内反复使用
- 空间局部性:在内存中邻近的数据接连被使用
- 缓存线:缓存一次读取多个数据
定义「缓存复杂度」 为处理大小为 的问题使用大小为 的缓存所产生的缓存未命中次数。算法可以利用缓存来提高效率:
- 缓存大小已知:算法可以取决于缓存大小
- 缓存大小未知:算法不能取决于缓存大小,要对所有缓存适用。这样的算法通常具有「分而治之」的思想
理论上,缓存大小未知也可以达成最优,和缓存大小已知的情况只差一个常数。
实例
矩阵乘法
- 简单:
- 缓存大小已知:
- 缓存大小未知:相同,但常数部分比较慢
矩阵加法
使用行优先和列优先等不同策略可以显著影响效率。